In this article, A comparative study of OCV (On Chip Variation), AOCV (Advance On Chip Variation) and POCV (Parametric On Chip Variation) have been done. Why and how a new variation model has evolved over the previous one and how it is better in terms of timing pessimism have also been discussed.
Introduction:
We have already discussed the On-Chip Variation (OCV) in a previous article. It is recommended that to go through that article to understand the OCV and its sources in a better way. Briefly, there are two types of process variations:
-
- 1. Systematic Variation (or Global Variation) and
- 2. Random Variation (or Local Variation)
Systematic variations are predictable in nature and could be modelled and tuned as the technology node get matured. But the random variation is highly unpredictable in nature and difficult to model it. Systematic variation is taken care in PVT and for random variation, we apply a derate factor on the delay of cells. Such a process variation could change the parameters of currents of the transistors and ultimately the delay of a cell. And if the delay of a cell gets affected it could result in the timing failure after fabrication and could result in post-silicon failure of a chip.
To avoid such failure and make the design immune from such process variation we have to keep the future process variation in mind and consider an expected delay variation while doing the Static Timing Analysis (STA).
On chip Variation (OCV):
In OCV a fixed timing derate factor is applied to the delay of all the cells present in the design so that in case of process variation affects the delay of any cells during the fabrication, it will not affect the timing requirements and the chip will not fail after fabrication.
Fabrication process variations could either increase or decrease the delay of a cell. So we need to set early and late values while setting the derate factor. STA tool would consider early or late timing derate based on the path and type of analysis. Here is an example of setting the OCV timing to derate factor.
% set_timing_derate -cell_delay-rise -data -early 0.92
% set_timing_derate -cell_delay-rise -data -late 1.10
% set_timing_derate -cell_delay-rise -clock -early 0.95
% set_timing_derate -cell_delay-rise -clock -late 1.06
% set_timing_derate -cell_delay-fall -data -early 0.90
% set_timing_derate -cell_delay-fall -data -late 1.12
% set_timing_derate -cell_delay-fall -clock -early 0.94
% set_timing_derate -cell_delay-fall -clock -late 1.07
In the above example, line-1 sets 8% early timing derate and line-2 sets 10% late timing derate to the rising edge on the data path. Similarly, line-4 and line-5 sets 5% early and 6% late timing derate to the rising edge on the clock path.
 |
| Figure-1: Derate factor on setup analysis |
 |
| Figure-2: Derate factor on hold analysis |
Figure-1 and 2, show the derate factor considered by the STA tool while setup and hold analysis for different paths. In reg2reg path timing analysis there is a launch flop from where data is launched and a capture flop where data is captured. The path between the clock source to the clock pin of the launch flop is called the launch clock path and the path from the clock source to the clock pin of the capture flop is called the capture clock path. In setup analysis worse case could be a late data path, late launch clock path and early capture clock path which could fail the setup timing. So STA tool will consider late timing derate for data path and launch clock path and early derate for the capture clock path.
For hold analysis, a fast data path, early launch clock and late capture clock could be the worst scenario. So STA tool will consider always the worst scenario and take the early derate factor for the data path and launch clock path and the late derate factor for capture clock path.
Issues in OCV:
Fixed timing derate used for all the cells in the OCV is over pessimistic. In reality, there is the cancellation of random variation effect. All the cells in a particular path could not be delayed all or early all. There is a mixed type of effect always and this causes cancellation of effect in total.
For example, consider a data path of 6 buffers and their typical delay is 20ps of each cell. Consider 20% late an early derate. So considering all the cells have the effect of late in delay, this path will have maximum delay 144ps. But in practice, it is very rare that all the cell will have an effect either late only or early only. Most likely some will be late and some will be early so there will be a cancellation of effect and real delay will always be less than 144ps. Figure-3 shows the delay variation with OCV derate factor.
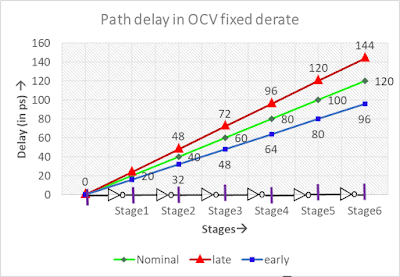 |
| Figure-3: Delay variation with OCV derate |
The concepts of OCV fixed derate was modelled in technology node above 90nm. It was good for such higher technology node. But in lower technology node and especially high-frequency designs, the timing closer became very difficult due to the high pessimism of fixed derate. So for the lower technology node, we need to resolve this issue. And so the concept of Advance On Chip Variation (AOCV) has evolved which does not use the fixed derate.
Advance On chip Variation (AOCV):
In AOCV derate is applied on each cell based on path depth and distance of the cell in the timing path and it also varies with cell type and drive strength of the cell. Distance is defined by a bounding box for the net and cells as shown in figure-4.
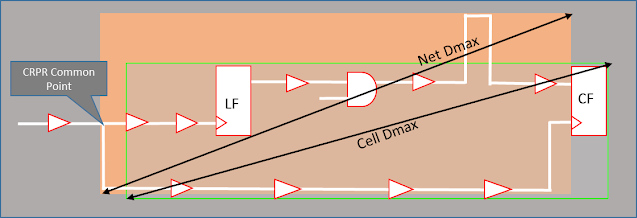 |
| Figure-4: Bounding box for cell and net distance |
Distance: If the distance increases, systematic variation would increase and to mitigate the variation, we need to use higher derate value. So along with the distance, derate value increases.
Path depth: In the case of distance is fixed and path depth increases, systematic variation would be constant but the random variation would tend to cancel each other. Therefore as path depth increases the derate factor would decrease. Figure-5, illustrate the path depth in the timing path.
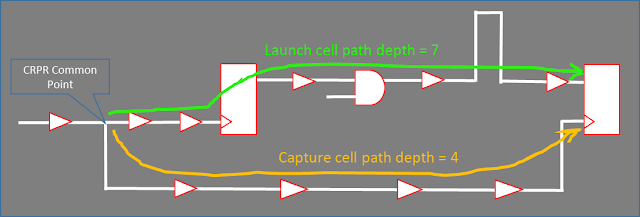 |
| Figure-5: Path depth in the timing path |
Cell type: The derate is based on the cell type as an AND gate and an OR gate can not exhibit the same variation. Derate value also varies with drive strength of the cell, like AND2X2 and AND2X6 will have different drive derate values.
AOCV Analysis Mode:
AOCV supports two analysis modes:
- 1. Clock only
- 2. Clock and data
In clock only mode, AOCV derate is applied only on the clock path so it has reduced effort and a fast runtime. Whereas in clock and data mode, AOCV derate is applied on full design. AOCV analysis requires an AOCV derate table for all the cells. Due to reduces timing pessimism in AOCV, it has been observed that huge time violations have been fixed when we moved to clock only AOCV derate mode and the violations have further reduced when we moved to clock and data AOCV mode.
AOCV analysis supports multiple AOCV derating table. There are generally two types of table are used either 1D table or 2D table. 1D table contains variation of derate values either with distance or depth whereas AOCV 2D derate table contains derate variation with both distance and depth together. An AOCV 2D derate table has shown in figure-6.
 |
Figure-6: AOCV 2D derate table example |
PrimeTime AOCV flow:
There are some additional steps added in AOCV derarte analysis as compared to OCV fixed derate flow. A flow of primeTime tool for AOCV derate analysis has shown in figure-7.
 |
| Figure-7: PrimeTime AOCV derate flow |
Issues in AOCV:
AOCV does not perform very well below 40nm technology node and to improve that we need to improve the timing pessimism further. Distance and Depth based derate factor used in the AOCV is good for technology nodes above 40nm but for the below node we need to improve it further. To address these issues Parametric On Chip Variation (POCV) has been developed. POCV is very effective in technology nodes 20nm and below.
POCV is a more realistic approach than that of OCV and AOCV. This method does not use distance and depth based derate factors. It uses delay sigma to model the delay variation of the cell. An advantage of POCV over AOCV is also that it reduces the slack pessimism between Graph-Based Analysis (GBA) and Path Based Analysis (PBA).
Parametric On chip Variation (POCV):
POCV advance variation technology provides statistical benefits without the overhead of expansive statistical library characterization. In POCV instead of applying the specific derate factor to a cell, cell delay is calculated based on delay variation (σ) of the cell. In POCV it is assumed that the normal delay value of a cell follows the normal distribution curve. An example of a normal distribution curve and standard deviation of data from the mean is shown in figure-8.
 |
| Figure-8: Standard deviation of data from mean |
In normal distribution 68% of data falls within the 1σ range, 95% data falls within 2σ and 99.7% data fall within the range of 3σ.
POCV Analysis:
- POCV uses a nominal delay value (µ) instead of using the min or max value of delay to model the random variations.
- Timing analysis is done using the nominal delay value (µ) and delay variation (σ) in the following way.
- Tool takes the value of σ from the timing library or an external file containing the POCV coefficient value C.
- Each arc time is then calculated statistically as the total of nominal delay and the variation.
- The tool then calculates the delay of the path by statistically combining these arc delay and perform the setup and hold timing analysis.
- By default, the tool performs the POCV analysis at 3σ from the mean but other values can also be specified. More the value of standard deviation, it’s more pessimistic in timing.
POCV input data:
The input for delay variation σ can be provided to the tool by the tool different ways as discussed below.
1. Using single POCV coefficient (C):
An external file containing the delay coefficient value C for each library cell, hierarchical cell or design. There is only one value of C for each timing arc of the cell irrespective of the input transition or output load. The delay variation σ is calculated based on C as follows.
The Delay variation (σ) = C * Nominal delay (µ)
An example of POCV coefficient file:
version: 4.0
ocvm_type: pocvm
object_type: lib_cell
rf_type: rise fall
delay_type: cell
derate_type: early
object_spec: */INV*
coefficient: 0.0693
2. Using Library Variation Format (LVF):
The information of POCV variation is directly provided into the library itself in LVF format. In LVF format there are two indexes used one for input transition and other for output load. An example of the POCV LVF format has shown below.
ocv_sigma_cell_rise (“pocv_template_4x4”) {
sigma_type : “late”;
index_1(“0.01, 0.04, 0.12, 0.80”);
index_2(“0.01, 0.02, 0.03, 0.10”);
values( “σ11, σ12, σ13, σ14”,
“σ21, σ22, σ23, σ24”,
“σ31, σ32, σ33, σ34”,
“σ41, σ42, σ43, σ44”, );
}
Typically index-1 denotes the input transition and index-2 denotes the output load.
If both data types are present in the design then by default the file with single POCV coefficient has higher precedence than POCV slew-load table or LVF format file.
POCV delay calculation:
Delay of a cell = Nominal delay (µ) ± (C * Nominal delay) * N
Where C = POCV coefficient and
N = Number of standard deviation
OR
Delay of cell = Nominal delay (µ) ± Variation
PrimeTime POCV analysis flow:
A flow of primeTime tool for POCV derate analysis has shown in figure-9.
 |
| Figure-9: PrimeTime POCV analysis flow |
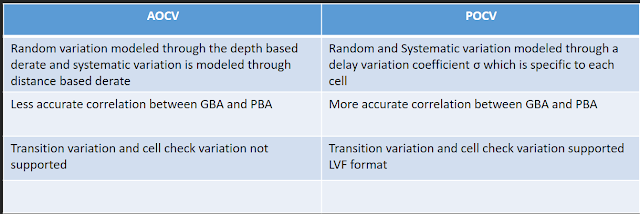
Comparison between POCV and AOCV:
A basic comparison between POCV and AOCV has shown below.
Summary:
In this article OCV, AOCV and POCV have been discussed in detail, The aim of this article is to provide the basic concepts of these three on chip variation methods and give a comparative insight.
Thank you!










Thank you!
Clear explanation,tq
Welcome
Thanks Sahu! Keep reading…
Thank you!
At the POCV, There are two different ways to calculate delay and what if there are two methods are both applied, then which priority is higher?
co-efficient file has precedence
how tool will pick nominaldelay ? is that delay from .lib timing library
Yes.
How cell type and drive strength of a cell having effect on OCV?
This comment has been removed by a blog administrator.
It's so clearly explained, thank you
Thank you.
Where in the .lib file I can find that information about LVF/coefficient?
I feel like the LVF table is better than a single coefficient for pessimism removal. So why tool prefer a coefficient number to LVF when both are present?
Also could u plz point out where in the LVF table we have related moment, skewness, and mean-shift data?
Could u plz explain what is moment/skewness/mean-shift in the normal distribution curve which is also related to LVF table? And how this is related to LVF for a tilted distribution curve?
Very helpful and detail explanation
Thank you very much.
An advantage of POCV over AOCV is also that it reduces the slack pessimism between Graph-Based Analysis (GBA) and Path Based Analysis (PBA).
Can you please explain the reasoning for this?
Hi Surya,
Thanks for asking this question.
I would like to say POCV is more effective at reducing slack pessimism than AOCV because it is more realistic and accurate. It also uses PBA, which is a more accurate method of timing analysis than GBA. This combination of factors makes POCV a more effective tool for timing closure.